Basics of 3D Geometry

The incentre of the triangle with vertices $\left(1\text{,}\sqrt{3}\right)$, $(0, 0)$ and $(2, 0)$ is

If the volume of a tetrahedron formed by the three coordinate planes and a variable plane is always $4$ cubic units, then the locus of the foot of the perpendicular from the origin to this variable plane is ${\left(x^2+y^2+z^2\right)}^3=kxyz$, where $k=$

Find the excenter opposite to vertex $C$ of triangle with vertices $A(3,4), B(0,0) \&\hspace{0.17em}C(-3,4)$.

Find the excenter opposite to vertex $B$ of triangle with vertices $A(3,4), B(0,0) \&\hspace{0.17em}C(-3,4)$.

Find the excenter opposite to vertex $C$ of triangle with vertices $A(20,15), B(0,0) \&\hspace{0.17em}C(-36,15)$.

Find the excenter opposite to vertex $B$ of triangle with vertices $A(20,15), B(0,0) \&\hspace{0.17em}C(-36,15)$.

Find the excenter opposite to vertex $A$ of triangle with vertices $A(20,15), B(0,0) \&\hspace{0.17em}C(-36,15)$.

A tracking station lies at the origin of a coordinate system with the $x$-axis due east, the $y$-axis due north and the $z$-axis vertically upwards. Two aircraft have coordinates $(20,25,11)\text{ and }(26,31,12)$ relative to the tracking station. The radar at the tracking station has a range of $40km$. Determine whether it will be able to detect both aircraft.

A tracking station lies at the origin of a coordinate system with the $x$-axis due east, the $y$-axis due north and the $z$-axis vertically upwards. Two aircraft have coordinates $(20,25,11)\text{ and }(26,31,12)$ relative to the tracking station. Find the distance between the two aircraft at this time.

Find the distance between the pair of points given below:

$\mathrm{A}(1,-2,10)$ and $\mathrm{B}(-4,0,3)$

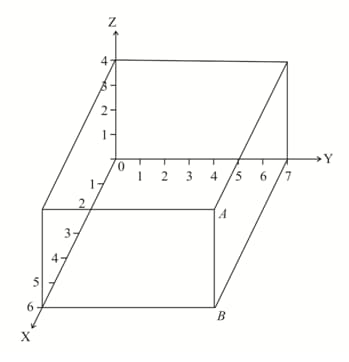
Find the coordinates of the midpoint, $M$, of the diagonal $\left[AO\right]$ of the cuboid.

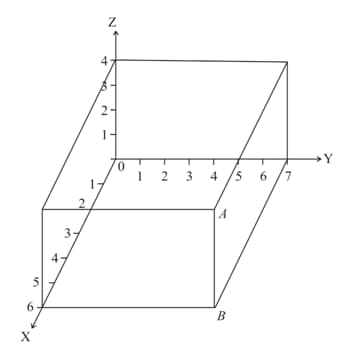
Write down the coordinates of point $A$ for the following cuboid:

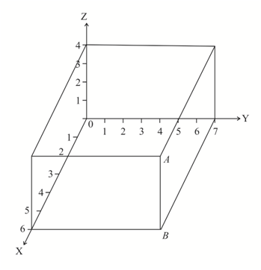
Write down the coordinates of point $B$ for the following cuboid:

Find the midpoint $M$ of the given points:

$A(-1,5,-4.2)$ and $\mathrm{B}(7,8.5,-11)$

Prove that the origin lies inside a triangle of which the three vertices are $(1, 2), (-2, 3)$ and $(-1, -4)$.

The base of a triangle passes through a fixed point $(f, g)$ and its other sides are bisected at right angles by the lines $y^2-8xy-9x^2=0$. Determine the locus of the vertex.

Find the Cartesian equation of the curve whose polar equation is $r^{1/2}=a^{1/2}\cos \frac{\theta }{2}$

The polar equation of a plane curve is $r=a \sin \theta +b \cos \theta$, where $a$ and $b$ are constants, find the Cartesian equation of the curve

If $\left(a, 0\right), \left(0, b\right)$ and $\left(1, 1\right)$ are collinear, then prove that $\frac{1}{a}+\frac{1}{b}=1$.

If the three points $(a, b), (a+k \cos \alpha , b+k \sin \alpha )$ and $(\alpha +k \cos \beta , b+k \sin \beta )$ be the vertices of an equilateral triangle, show that $\alpha ~\beta =\frac{1}{3}\pi$.